学习

博弈论

Normal form game 形式化定义一个可终止(Finite)的、有n 个主体参与的博弯为: \langle N, A, u\rangle 其中, - Players: N=\{1, \ldots, i, \ldots, n\} 表示参与博弯的主体 - Actions: A_i 表示Play

Normal form game

形式化定义一个可终止(Finite)的、有n 个主体参与的博弯为:

\langle N, A, u\rangle

其中,

- Players: N=\{1, \ldots, i, \ldots, n\} 表示参与博弯的主体

- Actions: A_i 表示Playeri 可以采取的动作集合，定义Action Profile为a=\left(a_1, \ldots, a_n\right) \in A=A_1 \times \cdots \timesA_n, 表示一个可能出现的情况

- Payoff function(Utility function, 效用函数): u_i: A \mapsto \mathbb{R} 表示Playeri 的Payoff function, 用来计算特定 Action Profile下Playeri 可以获取的回报；u=\left(u_1, \ldots, u_i, \ldots, u_n\right) 表示profile of utility function

最佳响应 Best Response

令a_{-i}=\left\langle a_1, \ldots, a_{i-1}, a_{i+1}, \ldots, a_n\right\rangle 表示除Playeri 外的其他所有Player选择的Actions，并将包含Playeri 在内的所有Player选择的Actions记为a=\left(a_{-i}, a_i\right)

对于某已知的a_{-i} ，其最佳响应集B R\left(a_{-i}\right) 定义为：

B R\left(a_{-i}\right)=\left\{a_i^* \mid \forall a_i \in A_i, u_i\left(a_i^*, a_{-i}\right) \geq u_i\left(a_i, a_{-i}\right)\right\}

即在已知所有其他Player选择的Actiona_{-i} 的情况下给Playeri 带来最大效用的a_i 的集合

纳什均衡 Nash Equilibrium

Pure Strategy 纳什均衡a=\left\langle a_1, \ldots, a_i, \ldots, a_n\right\rangle 定义为：

\forall i \in[1, n], a_i \in B R\left(a_{-i}\right)

即每个Player的Action均为Best Response的Action Profile

优势策略 dominant strategy

令S_{-i}=\left\{a_{-i}\right\} 表示除Playeri 外的其他所有Player所有可能Action的集合

策略s_i 严格优于(strictly dominates)s_i^{\prime} 定义为

\forall s_{-i} \in S_{-i}, u_i\left(s_i, s_{-i}\right)>u_i\left(s_i^{\prime}, s_{-i}\right)

策略s_i 弱优于(very weakly dominates)s_i^{\prime} 定义为

\forall s_{-i} \in S_{-i}, u_i\left(s_i, s_{-i}\right) \geq u_i\left(s_i^{\prime}, s_{-i}\right)

严格优于所有其他策略的策略称为优势策略

帕累托最优 Pareto Optimality

多目标优化问题的数学模型一般可以写成如下形式:

\begin{aligned} \min & f(x)=\left\{f_1(x), f_2(x), \ldots, f_n(x)\right\} \\ \text { s.t. } & x \in X \\ & X \subseteq R^m \end{aligned}

其中，f_1(x), f_2(x), \ldots, f_n(x) 表示n 个目标函数，X \subseteq R^m 是其变量约束的集合。

定义：解\mathbf{A}强帕累托支配解\mathbf{B}

假设现在有两个目标函数，解\mathbf{A} 对应的目标函数值都比解\mathbf{B} 对应的目标函数值好，则称解 \mathbf{A} 比解\mathbf{B} 优越，也可以叫做解\mathbf{A} 强帕累托支配解\mathbf{B}

定义：解\mathbf{A}能帕累托支配解\mathbf{B}

同样假设两个目标函数，解\mathbf{A}对应的一个目标函数值优于解\mathbf{B} 对应的一个目标函数值，但是解\mathbf{A}对应的另一个目标函数值要差于解\mathbf{B} 对应的一个目标函数值，则称解\mathbf{A}无差别于解\mathbf{B} ，也叫作解A能帕累托支配解\mathbf{B}

定义：最优解

假设在设计空间中，解A对应的所有目标函数值都达到最优，则称解A为最优解

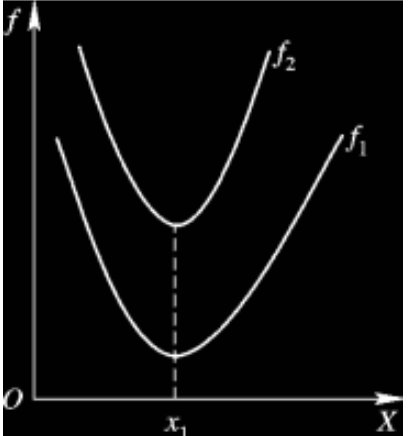
定义：帕累托最优解

假设两个目标函数，对于解A而言，在 变量空间 中找不到其他的解能够强帕累托支配解A，那么解A就是帕累托最优解（在其他任何解上都有一些目标函数值比解A差）（通常是一个范围）

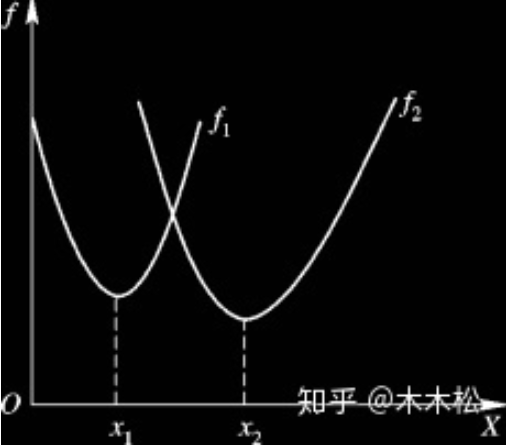
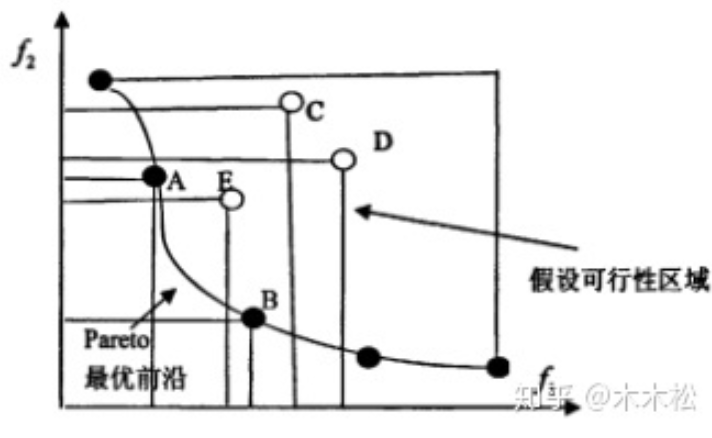
定义：帕累托最优前沿

帕累托最优解组成的集合

Mixed strategy

Mixed strategy是Action的概率分布。不同于Pure strategy中的策略a_i 定义为Playeri 从策略集A_i 中选择的某个 Action, Mixed strategy中的策略s_i 定义为Playeri 在策略集A_i 上的概率分布。

定义s_i 为Playeri 在策略集A_i 上的概率分布，s_i\left(a_i\right) 为Playeri 选择策略a_i 的概率，令a_{-i}=\left\langle a_1, \ldots, a_{i-1}, a_{i+1}, \ldots, a_n\right\rangle 表示除Playeri 外的其他所有Player选择的Actions，并将包含Playeri 在内的所有 Player选择的Actions记为a=\left(a_{-i}, a_i\right) 。那么, Mixed strategy下的纳什均衡s=\left\langle s_1, \ldots, s_i, \ldots, s_n\right\rangle 定义为:

\forall i \in N, \forall a_i \in A_i \quad \sum_a u_i(a) \prod_{j \in N} s_j\left(a_j\right) \geq \sum_{a_{-i}} u_i\left(a_{-i}, a_i\right) \prod_{j \in N, j \neq i} s_j\left(a_j\right)

很显然，不等式左边的u_i(a) 表示某个Action组合a 给Playeri 带来的效用，\prod_{j \in N} s_j\left(a_j\right) 是a 中的Actiona_j 在 Mixed strategy策略s_j 中的概率，所以很显然这一项是Action组合a 在Mixed strategy策略s_j 下发生的概率，所以整个\sum_a u_i(a) \prod_{j \in N} s_j\left(a_j\right) 这一项就表示所有Player的Mixed strategy策略给Playeri 带来的效用值的数学期望。

而不等式右边的的项很显然就是Playeri 确定选某个a_i 的情况下\left(s_i\left(a_i\right)=1\right) 的Mixed strategy策略给Playeri 带来的效用值的数学期望。

所以用人话将, Mixed strategy下的纳什均衡就是：所有Playeri 确定选择任何一个策略a_i 都不如Mixed strategy策略s_i 能带来更大的效用期望值。

Comment