我们可以假设有两个指针都指向起点，一个指针是慢指针，每次往后面移动一个，一个指针是快指针，每次往后面移动两个；

如果没有环存在，那么快指针一定先到最后的null处，退出；

如果有环存在，快指针一定会赶上慢指针

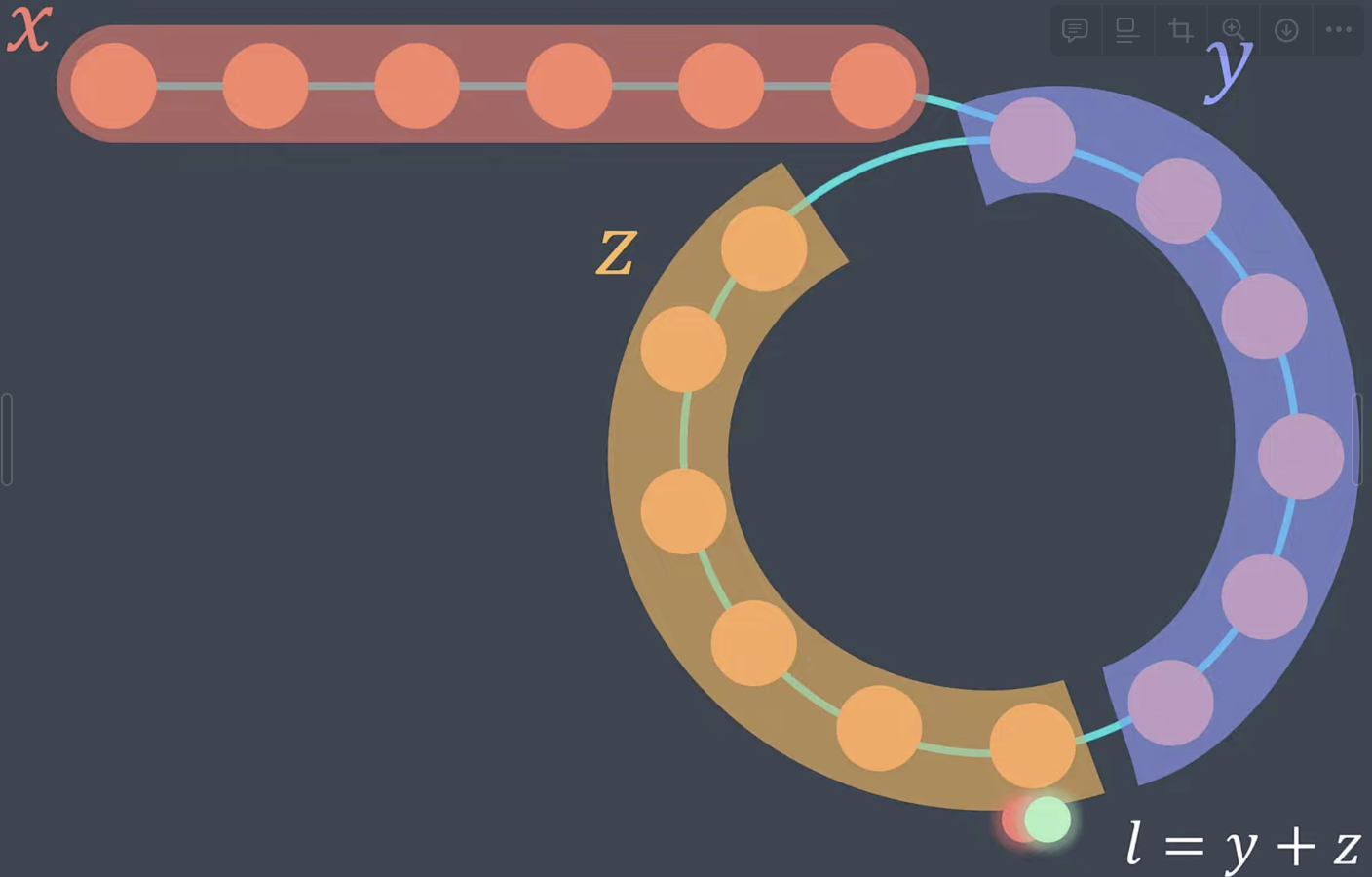
如果这个循环是存在的，我们假设快指针在某节点处赶上了慢指针，他距离起始节点(不包含)长度是z，整个环的长度是l，从起始节点(包含)到他们相遇的位置(不包含)长度是y，则有l=y+z。快指针已经走过的节点数量是f:fast，慢指针则是f:fast

那么因为每次快指针走的距离是慢指针两倍，f=2*s

那对于快指针就是先走了x，然后循环一定的圈数c_1然后再加上y赶上了慢指针

那对慢指针同理，循环圈数可能不一样

代入到f=2*s

因为l=y+z

2c_2-c_1-1 是个常量，我们假设他为c=2c_2-c_1-1

这意味着x的长度就是不知道多少轮圈循环的长度最后加上z，

那对于上个图的例子就是c=0，如果x够长，比循环圈还长就c>0

这有什么用呢，假如我们把慢指针放回最开始的head处，那么他和快指针同时按一个速度(一个节点一个节点)跳转，他们一定会相遇在循环开始的节点处！也就是慢指针走z步肯定会到循环开始的点(不知道z具体是多少的情况下就直接用指针判断相遇)

那么有个例子，假如有个arr数组，判断里面有没有重复的数字用O(1)的空间，对于这个数组，我们可以看到如果有重复，那么一定会有圈出现

func find_duplicate(arr []int){
	slow := 0
	fast := 0
	for {
		slow := arr[slow]
		fast := arr[fast]
		fast = arr[fast]
		if slow == fast{  //一旦相遇说明成环
			break
		}
	}
	slow = 0 // 会到头 找重复的那个值(下标)
	for slow!=fast{
		slow = arr[fast]
		fast = arr[fast]
	}
	return slow
}

那slow可不可以每次加3 加4？

结论：可以

我们可以假设fast是slow的k倍

环外x，环内l ，经过t次挪动：

slow在(t-x)\%l，

fast在(kt-x)\%l

当t=r*l也就是t是l也的某个整数倍的时候，且有模运算规则(a-b)\%c = (a\%c - b\%c)\%c，

slow可化简为(-x)\%l，fast也可化简为(-x)\%l，因此slow与fast相等相遇